mobility (muv)


This article is about the mobility for electrons and holes in metals and semiconductors. For the general concept, see Electrical mobility.
In solid-state physics, the electron mobility characterizes how quickly an electron can move through a metal or semiconductor, when pulled by an electric field. In semiconductors, there is an analogous quantity for holes, called hole mobility. The term carrier mobility refers in general to both electron and hole mobility in semiconductors.
Electron and hole mobility are special cases of electrical mobility of charged particles in a fluid under an applied electric field.
When an electric field E is applied across a piece of material, the electrons respond by moving with an average velocity called the drift velocity, \, v_d. Then the electron mobility μ is defined as
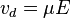\,v_d = \mu E.
Electron mobility is almost always specified in units of cm2/(V·s). This is different from the SI unit of mobility, m2/(V·s). They are related by 1m2/(V·s) = 104cm2/(V·s).
Conductivity is proportional to the product of mobility and carrier concentration. For example, the same conductivity could come from a small number of electrons with high mobility for each, or a large number of electrons with a small mobility for each. For metals, it would not typically matter which of these is the case, most metal electrical behavior depends on conductivity alone. Therefore mobility is relatively unimportant in metal physics. On the other hand, for semiconductors, the behavior of transistors and other devices can be very different depending on whether there are many electrons with low mobility or few electrons with high mobility. Therefore mobility is a very important parameter for semiconductor materials. Almost always, higher mobility leads to better device performance, with other things equal.
Semiconductor mobility depends on the impurity concentrations (including donor and acceptor concentrations), defect concentration, temperature, and electron and hole concentrations. It also depends on the electric field, particularly at high fields when velocity saturation occurs. It can be determined by the Hall effect, or inferred from transistor behavior.


Introduction

Drift velocity in an electric field

Main article: Drift velocity
Without any applied electric field, in a solid, electrons (or, in the case of semiconductors, both electrons and holes) move around randomly. Therefore, on average there will be no overall motion of charge carriers in any particular direction over time.
However, when an electric field is applied, each electron is accelerated by the electric field. If the electron were in a vacuum, it would be accelerated to faster and faster velocities (called ballistic transport). However, in a solid, the electron repeatedly scatters off crystal defects, phonons, impurities, etc. Therefore, it does not accelerate faster and faster; instead it moves with a finite average velocity, called the drift velocity. This net electron motion is usually much slower than the normally occurring random motion.
In a semiconductor the two charge carriers, electrons and holes, will typically have different drift velocities for the same electric field.
Quasi-ballistic transport is possible in solids if the electrons are accelerated across a very small distance (as small as the mean free path), or for a very short time (as short as the mean free time). In these cases, drift velocity and mobility are not meaningful.
Definition and units
See also: Electrical mobility
The electron mobility is defined by the equation:
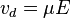\,v_d = \mu E.
where:
E is the magnitude of the electric field applied to a material,
vd is the magnitude of the electron drift velocity (in other words, the electron drift speed) caused by the electric field, and
µ is the electron mobility.
The hole mobility is defined by the same equation. Both electron and hole mobilities are positive by definition.
Usually, the electron drift velocity in a material is directly proportional to the electric field, which means that the electron mobility is a constant (independent of electric field). When this is not true (for example, in very large electric fields), the mobility depends on the electric field.
The SI unit of velocity is m/s, and the SI unit of electric field is V/m. Therefore the SI unit of mobility is (m/s)/(V/m) = m2/(V·s). However, mobility is much more commonly expressed in cm2/(V·s) = 10−4 m2/(V·s).
Mobility is usually a strong function of material impurities and temperature, and is determined empirically, mobility values are typically presented in table or chart form. Mobility is also different for electrons and holes in a given semiconductor.


Relation to conductivity

There is a simple relation between mobility and electrical conductivity. Let n be the number density of electrons, and let μe be their mobility. In the electric field E, each of these electrons will move with the velocity vector -\mu_e \mathbf{E}, for a total current density of n e \mu_e \mathbf{E} (where e is the elementary charge). Therefore, the electrical conductivity σ satisfies:[1]
\sigma=ne\mu_e.
This formula is valid when the conductivity is due entirely to electrons. In a p-type semiconductor, the conductivity is due to holes instead, but the formula is essentially the same: If p is the density of holes and μh is the hole mobility, then the conductivity is
\sigma=pe\mu_h.
If a semiconductor has both electrons and holes, the total conductivity is[1]
\sigma=e(n\mu_e+p\mu_h).


Examples

Typical electron mobility for Si at room temperature (300 K) is 1400 cm2/ (V·s) and the hole mobility is around 450 cm2/ (V·s).[2]
Very high mobility has been found in several low-dimensional systems, such as two-dimensional electron gases (2DEG) (3,000,000 cm2/(V·s) at low temperature),[3] carbon nanotubes (100,000 cm2/(V·s) at room temperature) [4] and more recently, graphene (200,000 cm2/ V·s at low temperature).[5] Organic semiconductors (polymer, oligomer) developed thus far have carrier mobilities below 10 cm2/(V·s), and usually much lower.